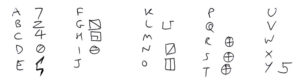
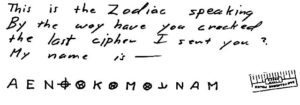In the wake of Dave Oranchak’s epic crack of the Zodiac Killer’s Z340 cipher, which other unsolved ciphers might get cracked in 2021?
For me, the way the Z340 was solved highlighted a number of issues:
- It seems very likely to me that other long-standing cipher mysteries will also require collaboration between entirely different kinds of researcher
- Hence I suspect that many are beyond the FBI’s in-house capabilities, and it will need to find a new way to approach these if it wants them cracked
- The whole Big Data thing is starting to open some long-closed doors
With these in mind, here’s my list of what might get cracked next:
Scorpion Ciphers
The Scorpion ciphers were sent to America’s Most Wanted host John Walsh from 1991 onwards: we have copies of S1 and S5, but the rest are in the hands of the FBI. As you’d expect, I’ve blogged about these many times, e.g. here, here, here, and here. I also created a related set of seven cipher challenges, of which only one has been solved (by Louie Helm) so far.

To be honest, I fail to understand why the FBI hasn’t yet released the other Scorpion Ciphers. These are the grist the Oranchak code-cracking mill is looking for: homophonic ciphers, underlying patterns, Big Data, etc.
Nick’s rating for a 2021 crack: 8/10 if the FBI releases the rest, else 2/10
Beale Ciphers
Even if I don’t happen to believe a measly word of the Beale Papers, I still think that the Beale Ciphers themselves are probably genuine. These use homophonic ciphers (albeit where the unbroken B1 and B3 ciphers use a system that is slightly different from the one used in the broken B2 cipher).
Because we already have the hugely improbable Gillogly / Hammer strings to work with (which would seem to be the ‘tell’ analogous to the Z340’s 19-repeat behaviour), we almost certainly don’t need to find a different book
Given that Virginia is Dave Oranchak’s stamping ground, I wouldn’t be surprised if the redoubtable Mr O has already had a long, hard look at the Beale Ciphers. So… we’ll see what 2021 has to bring.
Nick’s rating for a 2021 crack: 2/10
Paul Rubin’s Cryptograms
A curious cryptogram was found taped to the chest of Paul Emanuel Rubin, an 18-year-old chemistry student found dead from cyanide poisoning near Philadelphia Airport in January 1953. As usual, I’ve blogged about this a fair few times, e.g. here, here, here and here.
There’s a good scan of the cryptogram on my Cipher Foundation page here; there’s a very detailed account in Craig Bauer’s “Unsolved!”; and the 142-page FBI file on Paul Rubin is here.
The ‘trick’ behind the cryptogram appears to be to use a different cipher key for each line. Specifically, the first few lines appear to be a kind of “Trithemian Typewriter” cipher, where every other letter (or some such pattern) is enciphered using a substitution cipher, and where the letters inbetween are filled in to make these look like words. This is, I believe, the reason we can see words like “Dulles” and “Conant” peeking through the mess of “astereantol” and “magleagna” gibberish.
Right now, I’m wondering whether we might be able to iterate through thousands of possible Trithemian schemes to crack each individual line (e.g. lines 4 and 5 appear to share the same cipher key number).
The cipher keys appear to use security by obscurity (& terseness), so I suspect that these may well be defeatable. Definitely one to consider.
Nick’s rating for a 2021 crack: 4/10
Who was The Zodiac Killer?
Even if the Z340 plaintext failed to cast any light on his identity (as I certainly expected), surely a DNA attack must now be on the cards?
I’d have thought that the relatively recent (2018) success in identifying Joseph James De Angelo as the Golden State Killer must surely mean that the Zodiac Killer’s DNA is next in line in the forensic queue.
To my eyes, the murder of Paul Stine seems to me to have been the least premeditated of all the Zodiac Killer’s attacks, so I would have expected the crime-scene artifacts to have been a treasure trove of DNA evidence. But there are plenty of other claims for Zodiac DNA, so what do I know?
Anyway, I have no real doubt that there are 5 or 6 documentaries currently in production for 2021 release that are all racing to use DNA to GEDmatch the bejasus out of the Zodiac Killer. I guess we shall see what they find…
Nick’s rating for a 2021 breakthrough: 7/10 with DNA, else 0/10
Who Was The Somerton Man?
2021 may finally see the exhumation Derek Abbott has been pushing for for so long; plus the start of a worldwide DNA scavenger hunt to identify the unidentified corpse found on Somerton Beach on 1st December 1948.
But after all that, will the mysterious man turn out to be Robin McMahon Thomson’s missing father; or a shape-shifting Russian spy; or a Melbourne crim whom everybody suddenly wanted to forget they ever met?
All the same, even if we do get a name and a DOB etc, will that be enough to end all the shoddy melodrama around the case? Errrm… probably not. 🙁
For what it’s worth, I would have thought that Robin’s father’s surname was almost certainly (Nick shudders at the obviousness) McMahon. I also wouldn’t like to bet against a Dr McMahon in Sydney (e.g. the surgeon Edward Gerard McMahon, though I expect there are others), but feel free to enlighten me why you think McMahon was actually a family name etc etc.
Nick’s rating for a 2021 breakthrough: 8/10 with an exhumation, else 1/10