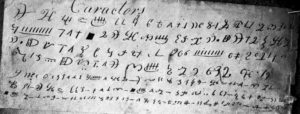“Cipher myth-making” and “cipher backfilling”…

by ⋅ 12 Comments

Having studied unsolved cipher mysteries for more than a decade, it seems to me that there are some distinct patterns of behaviour around them (by owners and by others) that serve to muddy the waters for modern researchers.

And so for the sake of collaborative clarity, I think that each of these behaviours ought to be given a ‘pattern name’. (There’s a very large “Patterns” literature in Architecture, Computer Science and Management, where common patterns of behaviour [both good and bad] are given names.) You may agree or disagree with the specific examples I give (and/or you may have a better pattern name in mind), but please hear me out, see what I’m trying to get at here…

“Cipher myth-making”

This behaviour typically occurs in the situation where someone has inherited or found an unsolved historical cipher, but has no provenance or definite historical context to work with. Unable to solve the cipher, the owner then (for whatever reason) concocts a myth or legend around it that they would like to be true.

The prime example here would seem to be the first version of “La Buse”‘s cryptogram (as famously described by Charles de la Roncière in his 1934 book “Le Flibustier Mysterieux”).

To my eyes, the odds are high that this was found in a notarial archive but with nothing accompanying it to help place or date it. And then, perhaps inspired by the early twentieth century Mauritian “gold rush” to find the Nageon de l’Estang pirate treasure, the owner presumed (though without proof) that it was a pirate treasure map.

My guess is that the myth that was added here was that of Olivier Levasseur hurling a treasure map into the crowd just before his execution, and exclaiming “Mon trésor à qui saura le prendre“. (There is, as far as I can tell, not a jot of evidence to support the idea that this melodramatic little scene actually happened.)

Without that, why would anyone link the cryptogram with La Buse?

“Cipher backfilling”

This behaviour occurs when the unsolved cipher has some kind of story already associated with it, but the absence of useful support details offers an evidential vacuum that demands to be filled in.

This differs from cipher myth-making in that here some kind of basic story needs to first be in place (though whether that story itself is true or false is another matter entirely): the additions are then in the form of elaborations to the core narrative, fleshing out its skeletal structure.

The obvious example of this would seem to be the second “La Buse” cryptogram:

Here, the elaborations would be the extra lines of cipher (some apparently cribbed from Poe), the drawings (some apparently cribbed from Howard Pyle), and the pigpen ciphertext saying “LA BUSE” (apparently cribbed from the myth).

The Beale Papers?

As with the two different “La Buse” cryptograms, the evidential haze around many other unsolved cipher mysteries can exhibit both cipher myth-making and cipher backfilling at the same time.

For example, I think there’s a strong argument that while the Beale Ciphers themselves could well be genuine, the case for the Beale Papers‘ being genuine is somewhat less straightforward.

The supposed bedrock of the history is that Beale placed an iron box with the cryptograms in trust with an innkeeper called Robert Morriss, who then opened it 23 years later (in 1845). However, the well-known problem with this timeline is that Morriss did not start work at the Washington Hotel until 1823, which was apparently after the box had already been left.

This suggests that Morriss may well have inherited the box from a previous innkeeper at the Washington Hotel: and that even if Morriss knew the correct name of the box’s owner (which was presumably, but not necessarily, written on the box itself), he may well never have actually met him.

This further suggests that Morriss may have taken the basic story about how Thomas Beale left a box at the Washington Hotel in the early 1820s and backfilled it until it became a tale worth telling and re-telling (while perhaps also advancing his personal claim on any treasure that may get found on it).

Moreover, it would seem that Morriss’s tale was then further elaborated by the (unnamed) author of the Beale Papers, until it became a tale worth printing (and hopefully buying).

However, if you put the Beale cryptograms to one side, I don’t currently see any evidence that anything about the Beale Papers is genuine, not even Thomas Beale’s name. Which perhaps goes to show how careful you have to be when trying to make sense of cipher mysteries.

The Voynich Manuscript?

It could well be that the the 1665 Marci letter that famously accompanied the Voynich Manuscript contains distant echoes of previous cipher myth-making: its suggested link to Roger Bacon now seems somewhat spurious, but was notable enough for Raphael Mnišovský to remember some decades later.

The supposed link between the Voynich Manuscript and John Dee / Edward Kelley is somewhat easier to deal with: without any real doubt, this was Wilfrid Voynich’s own cipher backfill. But his notion that the only conceivable way the manuscript could have travelled from England to Bohemia was via Dee and/or Kelley seems both historically and intellectually unsatisfactory.

Perhaps the bigger story here, as I’ve argued elsewhere, is that the Rosicrucian Manifestoes might possibly be the most extraordinary cipher backfill ever, i.e. that they were part of a huge after-the-event false history construction designed to appropriate the Voynich Manuscript into a scheme to con(vince) Holy Roman Emperor Rudolf II into backing a proto-Freemasonic group. But we may never be able to determine whether or not this is true.

Nowadays, there seems to be no end of people putting out YouTube videos and websites with Voynich-related backfill: indeed, perhaps the biggest challenge we face going forward is swimming through the brown tide of cipher backfill. Oh well!

The Spitalfields Mathematical Society, Augustus de Morgan, and an Astronomical Drinking Song…

by ⋅ 3 Comments

The other day, I was wondering where in East London (according to the story the owner told me) the Blitz Ciphers were found: and also wondered if they might have been left behind by some kind of mathematical society.

As an aside, the problem with any speculative mathematical link to Freemasonry is that even though Masonic theoretical historians like to talk about (capital-G) Geometry and how the Great Architect of the Universe (errrrm: God, basically) is somehow ineffably mathematical, their rather grand Platonic-Christian narrative breaks down when you bother to look at the details. The short version is that if there is any genuine maths in Masonry beyond basic Euclid-for-Dummies, it seems to me to be extraordinarily well-hidden.

(As always, if you happen to know of specific examples of mathematical Masonic societies that run counter to this sweeping generalization, please feel free to leave a comment below.)

So I instead went looking for genuine historical mathematical societies in London’s East End: and was delighted to discover the all-too-brief splendour of the Spitalfields Mathematical Society.

The Spitalfields Mathematical Society, Crispin Street

Conspiracy theorists and armchair cold case amateur detectives know this part of London well: the Ten Bells pub just around the corner was frequented by Jack the Ripper’s victims, the last of whom was found in Millers Court (close to Crispin Street). (Pastry chef geezer Jamie Oliver’s great-great-grandfather was for a while the Ten Bells’ landlord, for all you TV trivia fans.)

Incidentally, I found a rather nice website that blends historical photos of Spitalfields (taken by C. A. Mathew around 1912) with modern photographs taken on the same spot, to give an eerily evocative effect (such as the following image of Crispin Street):

But long before even C. A. Mathew, the history of the area revolved around Huguenot weavers, whose houses in Fournier Street are still there:

And it was the Huguenot immigrants who the Spitalfields Mathematical Society was originally aimed at, according to most accounts. De Morgan’s (1872) “A Budget of Paradoxes” describes it thus:

Among the most remarkable proofs of the diffusion of speculation was the Mathematical Society, which flourished from 1717 to 1845. Its habitat was Spitalfields, and I think most of its existence was passed in Crispin Street. It was originally a plain society, belonging to the studious artisan. The members met for discussion once a week ; and I believe I am correct in saying that each man had his pipe, his pot, and his problem. One of their old rules was that, “If any member shall so far forget himself and the respect due to the Society as in the warmth of debate to threaten or offer personal violence to any other member, he shall be liable to immediate expulsion, or to pay such fine as the majority of the members present shall decide.” But their great rule, printed large on the back of the title page of their last book of regulations, was “By the constitution of the Society, it is the duty of every member, if he be asked any mathematical or philosophical question by another member, to instruct him in the plainest and easiest manner he is able.” We shall presently see that, in old time, the rule had a more homely form.

I have been told that De Moivre was a member of this Society. This I cannot verify : circumstances render it unlikely ; even though the French refugees clustered in Spitalfields ; many of them were of the Society, which there is some reason to think was founded by them. But Dollond, Thomas Simpson, Saunderson, Crossley, and others of known name, were certainly members. The Society gradually declined, and in 1845 was reduced to nineteen members. An arrangement was made by which sixteen of these members, who were not already in the Astronomical Society became Fellows without contribution, all the books and other property of the old Society being transferred to the new one. I was one of the committee which made the preliminary inquiries, and the reason of the decline was soon manifest. The only question which could arise was whether the members of the society of working men for this repute still continued were of that class of educated men who could associate with the Fellows of the Astronomical Society on terms agreeable to all parties. We found that the artisan element had been extinct for many years ; there was not a man but might, as to education, manners, and position, have become a Fellow in the usual way. The fact was that life in Spitalfields had become harder : and the weaver could only live from hand to mouth, and not up to the brain. The material of the old Society no longer existed.

London had a fair few broadly similar societies – the Mechanic’s Institution and the London Architectural Society to name but two – but if you were looking for a mathematical society in East London that had long disappeared and some of whose papers might -possibly- have been the Blitz Ciphers, the Spitalfields Mathematical Society would seem to be at the very least an interesting candidate, right?

But the immediate question is…

Was Crispin Street bombed in WWII?

Having once idly flicked through a copy of “The London County Council Bomb Damage Maps 1939-1945” hardback when it came out in 2015, I half-remembered that the London bomb maps were all at the London Metropolitan Archive, and had once upon a time been in an exhibition there. There’s also tons more stuff in the National Archives in Kew (in whose downstairs bookshop I saw the book, incidentally).

But this being the Internet, there are also online bomb damage maps to try out. And it turns out that even though nearby streets were hit (such as Frying Pan Alley)…

…it would seem that Crispin Street escaped WWII unscathed.

So it would finally seem that we may well be out of luck with any possible connection between the Blitz Ciphers and the Spitalfields Mathematical Society. But all the same, I’m glad I looked. 🙂

And finally…

The Astronomer’s Drinking Song

Augustus De Morgan’s “A Budget of Paradoxes” includes the lyrics of a song sung at a Mathematical Society dinner in 1798, in honour of its solicitor, Mr. Fletcher. He had defended it against charges brought against them by “Informers”, but refused all offers of payment. Splendidly, De Morgan included the lyrics, which I reproduce below.

Of course, classic comedy song connoisseurs will instantly spot the connection with Monty Python’s “Rhubarb Tart Song“, which also mentions René Descartes (“The principles of modern philosophy / Were postulated by Descartes. / Discarding everything he wasn’t certain of / He said ‘I think therefore I am a rhubarb tart.’)

THE ASTRONOMER’S DRINKING-SONG.

WHOE’ER would search the starry sky / Its secrets to divine, sir,
Should take his glass I mean, should try / A glass or two of wine, sir !
True virtue lies in golden mean, / And man must wet his clay, sir ;
Join these two maxims, and ’tis seen / He should drink his bottle a day, sir !

Old Archimedes, reverend sage ! / By trump of fame renowned, sir,
Deep problems solved in every page, / And the sphere’s curved surface found, sir:
Himself he would have far outshone, / And borne a wider sway, sir,
Had he our modern secret known, / And drank his bottle a day, sir !

When Ptolemy, now long ago, / Believed the earth stood still, sir,
He never would have blundered so, / Had he but drunk his fill, sir :
He’d then have felt it circulate, / And would have learnt to say, sir,
The true way to investigate / Is to drink your bottle a day, sir !

Copernicus, that learned wight, / The glory of his nation,
With draughts of wine refreshed his sight, / And saw the earth’s rotation ;
Each planet then its orb described, / The moon got under way, sir ;
These truths from nature he imbibed / For he drank his bottle a day, sir !

The noble Tycho placed the stars, / Each in its due location ;
He lost his nose by spite of Mars, / But that was no privation :
Had he but lost his mouth, I grant / He would have felt dismay, sir,
Bless you ! he knew what he should want / To drink his bottle a day, sir !

Cold water makes no lucky hits ; / On mysteries the head runs :
Small drink let Kepler time his wits / On the regular polyhedrons :
He took to wine, and it changed the chime, / His genius swept away, sir,
Through area varying as the time / At the rate of a bottle a day, sir !

Poor Galileo, forced to rat / Before the Inquisition,
E pur si muove was the pat / He gave them in addition :
He meant, whate’er you think you prove, / The earth must go its way, sirs ;
Spite of your teeth I’ll make it move, / For I’ll drink my bottle a day, sirs !

Great Newton, who was never beat / Whatever fools may think, sir ;
Though sometimes he forgot to eat, / He never forgot to drink, sir :
Descartes took nought but lemonade, / To conquer him was play, sir ;
The first advance that Newton made / Was to drink his bottle a day, sir !

D’Alembert, Euler, and Clairaut, / Though they increased our store, sir,
Much further had been seen to go / Had they tippled a little more, sir !
Lagrange gets mellow with Laplace, / And both are wont to say, sir,
The philosophe who’s not an ass / Will drink his bottle a day, sir !

Astronomers ! what can avail / Those who calumniate us ;
Experiment can never fail / With such an apparatus :
Let him who’d have his merits known / Remember what I say, sir ;
Fair science shines on him alone / Who drinks his bottle a day, sir !

How light we reck of those who mock / By this we’ll make to appear, sir,
We’ll dine by the sidereal clock / For one more bottle a year, sir :
But choose which pendulum you will, / You’ll never make your way, sir,
Unless you drink and drink your fill, / At least a bottle a day, sir !

The Oak Island Ciphers (Part 1): the 80-foot rock cipher…

by ⋅ 21 Comments

It’s well-known that over the last two centuries, the quest for the mysterious “Money Pit” on Oak Island has yielded no sign of treasure while simultaneously consuming an inordinate quantity of diggers’ dollars – and if you can even think about all that without silently mouthing the phrase ‘ironically enough’, you have a huge amount of self-control. 😉

Yet despite all that ‘activity’, nothing of any actual substance about the whole curious enterprise that put or left the (so-called) pit there in the first place seems to have emerged. All that has been achieved is that (a) a small island has been ravaged by glinty-eyed treasure hunters, and (b) bookshelves have been filled with books that almost all manage to leave readers somehow less knowledgeable than when they began.

If you pause to reflect on the scale and prolonged fruitlessness of this archaeological disaster zone even momentarily, you’ll surely find it hard to prevent the two words “Epic” and “Fail” from lurching to the front of your mind. 😐

“The Curse of Oak Island”

Perhaps naturally enough, it seems that the (apparently obligatory) combination of determination, hubris, cupidity and stupidity that Oak Island treasure hunters have also makes them ideal Reality TV subjects, every bit as good as the Kardashians, TOWiE or whatever. Which is why the Canadian reality TV show “The Curse of Oak Island” (which premiered in 2014, and follows the Oak Island treasure hunt being pursued by Michigan brothers Marty and Rick Lagina) is now in its fantabulous 4th season. Will it ever end? (What do you think?)

Whatever you personally make of the whole Oak Island reality TV project, it is surely a brutal mirror to hold up to modern culture’s pox-plagued visage: for if all it boils down to is a fruitless search for something that nobody can describe and for which there seems to be no actual evidence, surely nobody involved can emerge the other side looking or smelling good. 🙁

Yet, curiously paralleling the Anton Transcript at the core of Mormonism, at the heart of the Money Pit mythology lies a cipher mystery that has had so much screen time in Z-grade historicalist documentaries that it practically has its own Equity card. Yes, I’m talking about a cipher that could get gigs on cruise ships.

As per normal, nobody knows whether or not this cipher is the real deal or merely Milli Vanilli. Moreover, it turns out that – just like the two versions of La Buse’s cryptogram – it also has a secret twin cipher (and nobody knows whether or not that’s real either), which we’ll (eventually) return to in Part 2. 🙂

Anyhoo, it’s time we all had a proper Cipher Mysteries look at the first (and infamous) Oak Island cipher…

The 80-foot Rock Cipher

Though most modern authors call it the “90-foot rock” cipher, this was claimed to have been found carved into a rock found eighty feet underground. As usual, I try to avoid following trends if I know they’re broken. 🙂

Regardless, the first documentary mention of it is in a 2nd June 1862 letter written by treasure hunter Jotham B. McCully of Truro, printed in the “Liverpool Transcript” in October 1862 in response to a critical article entitled “The Oak Island Folly”. McCully wrote “The Oak Island Diggings” to explain why he and the other treasure hunters were so convinced there was treasure in the Pit.

Bearing in mind that, according to other records, the original ‘Onslow Company’ search started in about 1795…:

“About seven years afterwards, Simeon Lynds, of Onslow, went down to Chester, and happening to stop with Mr. Vaughn, he was informed of what had taken place. He then agreed to get up a company, which he did, of about 25 or 30 men, and they commenced where the first left off, and sunk the pit 93 feet, finding a mark every ten feet. Some of them were charcoal, some putty, and one at 80 feet was a stone cut square, two feet long and about a foot thick, with several characters on it.”

According to this admirably source-heavy webpage, the stone was “yet to be seen in the chimney of an old house near the pit” (19th February 1863, Yarmouth Herald).

Then, the “remarkable” stone was then revealed to have been found “pretty far down in the pit, laying in the centre with the engraved side down”, and the house was revealed to be that of John Smith. It contained “a number of rudely cut letters and figures upon it. They were in hopes the inscription would throw some valuable light on their search, but unfortunately they could not decipher it, as it was either too badly cut or did not appear to be in their own vernacular.” (2nd January 1864, The Colonist, Halifax N.S.)

George Cooke, in a 27th January 1864 letter, described the marks as “rudely cut letters, figures or characters […]. I cannot recollect which, but they appear as if they had been scraped out by a blunt instrument, rather than cut with a sharp one.” He hoped that they could be deciphered in the future.

But what did the marks say? At that point in the cipher’s history, it seems nobody had decrypted it. But, according to the Oak Island Treasure Company prospectus (the copy transcribed on pp.215-225 of Geoff Bath’s “Maps, Mystery, and Interpretation” [Part 2] is dated 1894):

Many years afterwards, it was taken out of the chimney and taken to Halifax to have, if possible, the characters deciphered. One of the experts gave his reading of the inscriptions as follows: “Ten feet below are two million pounds buried.” We give this statement for what it is worth, but by no means claim that this is the correct interpretation. Apart from this however, the fact remains that the history and description of the stone as above given have never been disputed.”

Hence it was (apparently) first decrypted between 1864 and 1894.

Creighton’s Bookstore

The next mention of the “quaint carven stone” has it in Creighton’s Bookstore in Halifax, N.S.: “but the inscriptions were erased long ago after the stone had endured the blows from a bookbinder’s mallet. But at the time of the discovery of the stone the inscriptions were translated to read: ‘Ten feet below, 2,000,000 pounds lie buried.'” (29th April 1909, Fairbanks Daily News Miner).

Yet… the 19th August 1911 edition of Collier’s Magazine contains an eyewitness account supplied by Captain H.L. Bowdoin that departs somewhat from the dominant narrative. He wrote:

“While in Halifax we examined the stone found in the Money Pit, the characters on which were supposed to mean: “Ten feet below two million pounds lie buried.” The rock is of a basalt type hard and fine-grained.”

“There never were any characters on the rock found in the Money Pit. Because: (a) The rock, being hard, they could not wear off. (b) There are a few scratches, etc., made by Creighton’s employees, as they acknowledged, but there is not, and never was, a system of characters carved on the stone.”

There was backed up thoroughly by a 27th March 1935 eyewitness statement by Harry W. Marshall, who was the son of one of the owners of Creighton & Marshalls:

One of the Creighton’s was interested in the Oak Island Treasure Co. and had brought to the city a stone which I well remember seeing as a boy, and until the business was merged in 1919 in the present firm of Phillips & Marshall. The stone was about 2 feet long, 15 inches wide, and 10 inches thick, and weighed about 175 pounds. It had two smooth surfaces, with rough sides with traces of cement attached to them. Tradition said that it had been part of two fireplaces. The corners were not squared but somewhat rounded. The block resembled dark Swedish granite or fine grained porphyry, very hard, and with an olive tinge, and did not resemble any local stone. Tradition said that it had been found originally in the mouth of the “Money Pit”. While in Creighton’s possession some lad had cut his initials ‘J.M.” on one corner, but apart from this there was no evidence of any inscription either cut or painted on the stone. Creighton used the stone for a beating stone and weight. When the business was closed in 1919, Thos. Forhan, since deceased, asked for the stone, the history of which seems to have been generally known. When Marshall left the premises in 1919, the stone was left behind, but Forhan does not seem to have taken it. Search at Forhan’s business premises and residence two years ago disclosed no stone. The full history of the stone was written up in ‘the Suburban” about 1903 or 1904.

(Incidentally, people have searched for this issue of “The Suburban” but without any success.)

The two stones

Nobody seems to have dwelt much on what – to me, at least – is the most obvious problem with the above. Which is that we seem to be talking about two quite different stones here.

The first stone: “a stone cut square, two feet long and about a foot thick”, found eighty feet underground, and put into a chimney. Has curious writing on. Repeatedly described as having been “cut square”, like a “flagstone”.

The second stone: “2 feet long, 15 inches wide, and 10 inches thick”, “rounded” corners, found near the mouth of the Money Pit, and had been taken out of a chimney. Apparently has no writing on. “Basalt type hard and fine-grained” (Bowdoin), or “dark Swedish granite or fine grained porphyry, very hard, and with an olive tinge” (Marshall).

While it is entirely possible that the first stone was cut down to make it fit in John Smith’s chimney, the two descriptions don’t seem to fit each other in any other way either.

The most likely explanation to my mind is that we are talking about two entirely separate rocks both coming from the Money Pit, the first with marks roughly carved into it (and so perhaps a softer stone such as sandstone), and the second a much harder stone with no marks carved into it (the “JM” was added during its time in Halifax).

The first stone may therefore still be extant somewhere, perhaps in the garden of a Halifax house of a former treasure hunter.

Images of the 80-foot rock cipher

The short version is that there are no tracings or copies made from the object itself whose veracity we can be even remotely sure of: most of the images floating round the Internet are mock-ups of what people think it should look like.

Worse, the cipher’s plaintext seems to have changed along the way. Whereas in 1894 it was described as saying “Ten feet below are two million pounds buried”, this later changed into “Forty feet below two million pounds are buried” – note both the different depth and the different word order.

Where did this change? The first time we see the “forty feet” version is in a circa 1949 typewritten account of Oak Island by Reverend Austen Tremaize Kempton (which was never published):

Here’s what it looked like in print (I believe this is in Edward Rowe Snow’s 1949 “True Tales of Buried Treasure”):

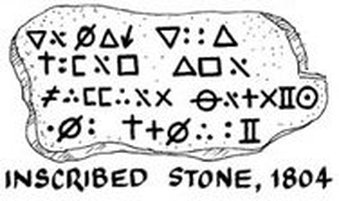
The person now often said to have decrypted the inscription was Dalhousie University Professor of Languages James Leitchi: there’s a good-sized page on him here.

Of course, one problem with this is that Leitchi was not actually an “old Irish school Master” but Swiss. However, he was (according to the timeline) a teacher at Halifax High School up until 1884: and we know that the stone was decrypted in Halifax before 1894.

Analyses and theories

Even though there is essentially zero doubt that the cipher as presented by Kempton (and then Snow) does indeed read “Forty feet below two million pounds are buried”, plenty of extra interpretations (typical “dual cipher” theories) have been put forward. One such was Dr. Wilhelm’s (modified) “At eighty guide maize or millet estuary or firth drain F”, described here.

Other webpages suggest that the letter shapes are all mathematical symbols, but this seems a bit lame to me: the shapes are just simple cipher shapes, nothing funky.

Other webpages suggest that Kempton faked the cipher, or that the whole thing is in fact a Masonic cryptogram or riddle. There’s also a theory by Keith Ranville, who also once put forward a Silk Road prostitution theory about the Voynich Manuscript

But I think all these theories and ideas are missing the big problem: which is that because we can’t account for the change in wording between the two versions of the cipher, we simply can’t comfortably trust the versions we have.

However, it’s entirely possible that I’ve missed something important in all the timelines. Please let me know if I have, thanks! 🙂

Might the Z408 Zodiac Killer cipher be a clue to a book?

by ⋅ 21 Comments

In a recent post here, I floated the idea that the Zodiac Killer’s Z408 (solved) cipher’s unusual homophone distribution may have arisen not conceptually (i.e. from a hitherto-unknown book on cryptography), but instead empirically (i.e. emerging from the properties of a specific text).

It’s certainly possible that he might have used his own (private) text to model his homophone distribution, in which case we probably almost no chance of reconstructing it. However, I think it likely that he instead used the first few characters of an already existing public text (such as Moby Dick, the Book of Genesis, the Declaration of Independence, or whatever) to do this.

It’s a reasonable enough suggestion, I think: and moreover one that we can try to test to a reasonable degree.

Z408’s homophones

A homophonic cipher key allocates a number of cipher shapes to individual plaintext letters, usually (but not always) in broad proportion to their frequency. So in a typical homophonic cipher key you would expect to see far more shapes for E (the most common letter in English) than for, say, Z or Q.

Though this is essentially the case for what we see in the Z408 cipher (particularly for the more frequent letters, ETAOINS), the numbers of homophones chosen for the less frequent letters seem somewhat idiosyncratic and arbitrary:

7 shapes – E
4 shapes – T A O I N S
3 shapes – L R
2 shapes – D F H
1 shape  – B C G K M P U V W X Y
Did not appear: J Q Z

People have long searched for a primer or textbook on cryptography where the description of the alphabetic frequency distribution matches this, or even where the alphabetic frequency ordering (e.g. ETAOINSHRDLU etc) matches the order here, but in vain.

Designing a filter

The basic idea for the filter is easy enough:
* read in characters from the start of a passage (we’re only interested in capitalized alphabetic letters, i.e. A-Z)
* if the instance count of that character is higher than the top of the desired range, then the test fails
* if the instance counts for all the characters are within the desired range at the same time, then the test passes
* else keep reading in more characters until the test terminates

As a side note: of all the Z408 homophones, only X appears exactly once in the Z408 ciphertext itself: but while it is conceivable that the Zodiac Killer might have allocated extra homophones for X, it does seem fairly unlikely.

The desired ranges for each of the characters would look like this (though feel free to adapt this if you disagree with the homophone counts listed above):

[7,7] – E
[4,4] – T A O I N S
[3,3] – L R
[2,2] – D F H
[0,1] – B C G K M P U V W Y J Q Z
[0,3] – X (to err on the side of safety)

Note that the single-letter characters have a slightly broader [0,1] range because we have no way of knowing whether or not they would have actually appeared in the original text.

Here are two test texts that should both pass:

EEEEEEETTTTAAAAOOOOIIIINNNNSSSSLLLRRRDDFFHHZZZZZZZZZZZZZZZZZ

BCGKMPUVWYJQZXEEEEEEETTTTAAAAOOOOIIIINNNNSSSSLLLRRRDDFFHHZZZ

Which texts to try?

Though any text published before August 1969 would potentially be a match, it would make sense to look at all manner of texts, and possibly even the first few lines of different chapters of books (though I’d be a little surprised if that was the case). All the same, the filter is easy enough to write (and should execute in a matter of microseconds) and to test, so the difficulty here lies mostly in getting hold of enough texts to try, rather than the compute time as such.

Oddly, I don’t really have a solid feel for how often the filter will find a match: my gut instinct is that roughly one in a million English text comparisons will pass, but that’s just a guesstimate based on each letter having its own little bell-curve distribution, all of which have to match at the same time.

So what do you think will match? “Catcher in the Rye” or “Moby Dick”? Place your bets! 😉

A new clue for the d’Agapeyeff Challenge Cipher…?

by ⋅ 2 Comments

A little while back, I had a email from Marie about Alexander d’Agapeyeff’s (1939) book “Codes and Ciphers”, highlighting some interesting mistakes she had found in his section on double transposition cipher.

D’Agapeyeff described this as a cipher system that the Russian Nihilists had used, but said that they had used the same keyword for both halves of the transposition (i.e. for transposing both the columns and the rows), a technical flaw that made it easy to crack. (Oddly, the Nihilists are nowadays associated with an entirely different kind of encipherment.)

Let’s take a closer look…

D’Agapeyeff’s Double Transposition

What follows is d’Agapeyeff’s account, with comments along the way.

At the end of the nineteenth century the Russian Nihilists used a double cipher, which, having been transposed vertically, was then transposed horizontally; but they made the mistake of using the same keyword in both transpositions. As it is a common variation of double columnar cipher, we give it as an example:

The first thing that Marie picked up on was that the way that d’Agapeyeff converted the transposition keyword SCHUVALOF to an ordering was clearly incorrect: F is the sixth letter of the alphabet, so there is no obvious way that it would be counted as the highest ranked of the nine letters in the keyword. When I looked at this, I immediately guessed that it should instead have read SCHUVALOV – as it turned out, this was a good try, though still very slightly wrong. 😐

Regardless, it should already be clear that something a little non-obvious is going on here.

Now suppose we have to encipher the following: ‘Reunion to-morrow at three p.m. Bring arms as we shall attempt to bomb the railway station. Chief.’

The ‘abcd’ at the end are ‘nulls’ used to fill in the squares.

Now we transpose the message according to the letter sequence of the keyword:

So the message reads:

OMPBOETTMWORATMROTMREBRHEPIATHILBERWTYSIOATANOEUNTRNIOSGAASNRMWLSHATEALTAHIBCCEFD

In all languages where certain letters must follow or precede certain others, the deciphering of this script will never present difficulties. We first count the number of letters in the script (81), which will give us the size of the square (9×9), and once this is done all we have to do is remember that in nine cases out of ten ‘h’ follows either ‘t’ or ‘s’ or ‘c’, and that the bigrams such as AT, TO, WE and the very helpful (English) trigram ‘the’, and the doubles TT, LL, EE, etc., are the most common. In fact, the Russian police soon found out all about that conspiracy.

The second thing Marie noted here was that d’Agapeyeff was using the double transposition decryption direction here, rather than the encryption direction.

All in all, I’d agree with Marie that d’Agapeyeff didn’t seem to have fully understood how the system worked. Smartly, though, Marie now doggedly decided to look at d’Agapeyeff’s crypto sources, to see if he had copied this whole section blindly from somewhere. And, eventually, she found that d’Agapeyeff’s direct source for the above was none other than…

Auguste Kerckhoffs

…the Dutch cryptographer Auguste Kerckhoffs (1835-1903).

Kerckhoffs’ influential book (well, extended article, really) “La Cryptographie Militaire” is available online as a PDF, or as an HTMLized version here.

What follows is my usual free translation of Kerckhoffs’ description of double transposition, which we can immediately see beyond any reasonable doubt as being the source for d’Agapeyeff’s version:

On the occasion of the Nihilists’ last appearance in court, the Russian newspapers published the accused’s secret cipher. It is a system of double transposition, where the letters are first transposed by vertical columns, and are then further transposed by horizontal rows. The same word serves as a key for both transpositions: to do this, the keyword is transformed into a series of numbers, where each number matches the rank of the letter within the normal alphabetical sequence.

Here is the process applied to the word SCHUVALOW:

OK, though I was on this occasion very slightly wrong (SCHUVALOV rather than SCHUVALOW), I was at least wrong in the right kind of way. 🙂 Kerckhoffs continues:

Now, if we were to transpose a sentence such as this one – Vous êtes invité à vous trouver ce soir, à onze heures précises, au local habituel de nos réunions – we would proceed first as in the previously described [single transposition] case, and then carry out the same operation for the horizontal rows.

   = s c i a u e s e l a v i v o n t e u v t r e r s o u c a c a b i o l h t n e l o s u d e r, etc.

However complicated this transposition may appear to us, deciphering a cryptogram written with this system, can never present insurmountable difficulties in languages ​​where certain letters only present themselves in particular combinations, such as q or x in French. Here, the Russian decipherers seem to have carried out their decryption work in a relatively short time.

For any passing conlang fans, Auguste Kerckhoffs was also closely associated with the artificial language Volapük, which some people think is really koldälik. 🙂

d’Agapeyeff + Kerckhoffs = …?

It’s important to remember that d’Agapeyeff wasn’t himself a cryptographer, but rather someone who was trying to collect together interesting crypto stuff into a book that had originally been commissioned for someone else entirely to write. The project wasn’t something he was aiming to do, but rather something that fell in his lap.

As Marie points out, the big technical thing that d’Agapeyeff got wrong is that the numbers are the wrong way round, and so he is performing a double transposition decryption rather than a double transposition encryption: the two are not the same at all. That is, if you used SCHUVALOW as your single transposition keyword and then single transposition encrypted the text “SCHUVALOW”, you should get the ciphertext “ACHLOSUVW”: but both Kerckhoffs and d’Agapeyeff (copying Kerckhoffs) seem to have got this the wrong way round.

Having thought about this for a little while, I’ve come to suspect that d’Agapeyeff may well have faultily believed that double transposition was a self-inverse process, i.e. where the decryption and encryption transformations are identical.

All of which would dovetail very neatly indeed with the report that we have that he was unable to decrypt his own challenge cipher: for if he (wrongly) believed that double transposition was self-inverse, then he wouldn’t (if his challenge cipher had used double transposition) have been able to decrypt it at all. If this is correct, then his failure wasn’t anything as foolish as misremembering the keyword, but instead misunderstanding one of the component ciphers that made up the overall chain.

Might this insight help us decrypt his challenge cipher? Well… insofar as it now seems far more likely to me that he used double transposition as one of his stages, then the answer may very well be yes. Hopefully we shall see… 🙂

Reconstructing Lee Erwin Shackelford’s family tree…

by ⋅ 201 Comments

Prolific (if occasionally prolix) Cipher Mysteries commenter bdid1dr has long wondered whether the Somerton Man was someone in her ex-husband’s family. (She also suspects her ex-husband was the infamous Zodiac Killer, but let’s leave that for another day.)

Even though it at first sounds like an outrageously long shot (and one that would perhaps necessitate a Warren Commission ‘magic bullet’), it does in fact concord with many of the things we know about the Somerton Man, in perhaps surprising ways.

For a start, the aluminum comb, the packet of Juicy Fruit chewing gum found in the Somerton Man’s American-stitched coat and indeed the coat itself have all been taken as suggesting that the Somerton Man was American (or had recently travelled from America).

More specifically, Derek Abbott launched his recent (but unsuccessful) crowdfunding campaign on the back of a fragmentary DNA match between one of the hairs found embedded in the plaster cast bust of the Somerton Man and Thomas Jefferson.

Yet it turns out that the Shackelfords are an old Virginian family… with links to Thomas Jefferson. OK, this is all still very far from proof, but we’re not yet veering into anything like the canonical Lands Of Somerton Nonsense: so please bear with me just a little longer as we take a look at the Shackelfords…

Lee Erwin Shackelford

According to the Sydney Morning Herald, he was born on 12th April 1945 to Willian Shackelford and Normaleen (nee Park):

SHACKELFORD (nee Normaleen Park). April 12, King George V Hospital, Camperdown, semi-private, wife of T./Sgt. W. Shackelford, U.S. Air Corps – a son (both well)

And thanks to a little archival magic (big tips of the Cipher Mysteries hat to Eye and Aye for this), we have a photo of Lee Erwin Shackelford from the USS Ticonderoga circa 1964:

He was also bdid1dr’s first husband: she says that he died in New York a few years ago.

He had a brother (Preston Park Shackelford) who was born 10th April 1948 in Vallejo CA: and another brother (Mark) who was born in New Mexico in 1952.

William Jesse Shackelford Jr

Eye and Aye came up trumps here as well, with William Jesse Shackelford Jr’s US Armed Forces registration card (note: image behind a Fold3 paywall). According to this, he was born on 17th May 1922 in Norfolk VA: the “Name And Address Of Person Who Will Always Know Your Address” field is marked up as “Mrs A. B. Shackelford, 1631 Willoughby Ave, Norfolk, VA”. (Willoughby Ave is close to Norfolk’s Lyon Shipyard: #1631’s plot was long since sacrificed to make way for the I-264.)

According to the Registrar’s Report (note: image also behind a Fold3 paywall), William Shackelford Jr was white, 5′ 5″, 125 lbs, hazel eyes, brown hair, and with a ruddy complexion. He received his honourable discharge from the Army on the 30th August 1945 (ref: 13-062-516).

Unless he secretly had access to a Tardis, William Shackelford was not the Somerton Man: he was still very much alive in 1950, 1960, and even 1970.

Misca pointed out that:

On ancestry there is a record of a Normaleen May Shackelford travelling from Brisbane to San Francisco with her son Lee Ervin/Erwin. The name of the friend/relative she states she is visiting is William Shackelford, 835 Oaklette Avenue, Norfolk, Virginia. A 1940 census document shows two William J Shackelfords living on Oaklette. One is 39 and the other is 17. Father and son. Further research shows the son as having been in the US Airforce in WW II. He is William Jesse Shackelford. He married three times. First wife unknown but I suspect it may have been Normaleen. Second wife (married in 1957) Leila Barnes Stewart (who seems to have died), third wife Catherine Anne Garrett.

William Jesse Shackelford Sr

William Jesse Shackelford Sr’s obituary (in the 7th December 1972 Virginia Beach Sun looked like this:

William Jesse Shackelford, 73, of 292 Stancil St., Princess Anne Plaza, an insurance agancy [sic] operator, died in a hospital November 28 after a long illness.
He was a native of Walter Valley, Tex., a son of William J. and Mrs Martha Farley Shackelford, and the husband of the late Mrs Josephine Taylor Shackelford.
He was the owner of William J. Shackelford Insurance Co. He was a member of Norfolk Elks Lodge 38, American Legion, and Commodore FOP Lodge 3.
He was a World War I veteran.
Surviving are two daughters, Mrs Bennie S. Jordan of McLean and Mrs Shirley S. Becker of Virginia Beach; a son, William Jesse Shackelford Jr of Alexandria; two sisters, Mrs Cordelia Willcox of Tuolumne, Calif., and Mrs Sylvia S. Snyde of Corpus Christi, Tex.; a brother, Feilx Shackelford of Odessa, Tex.; 11 grandchildren; and 11 great grandchildren.

Might there be a missing Shackelford…?

I hope it’s not construed as unkind of me to note that bdi1d1dr’s handed-down family stories don’t quite add up. At this remove in both time and space, tales about her ex-husband’s family’s life in Australia (he moved to the US at a very young age) are bound to be fragmentary and incomplete.

What is either interesting or just plain Chinese Whispered here is that she was sure that there was also a Lee Irving Shackelford in Australia, who somehow disappeared: and quite how he fits into the whole picture nobody seems to know or remember.

And so my challenge to you fine people is to find out if there was a disappearing relative in William Jesse Shackelford (Jr or Sr)’s immediate family tree. Oh, and who was “Mrs A. B. Shackelford”?

Incidentally, one unusual (but possibly useful) resource here is the Shackelford Clan, a group that published a family history newsletter from May 1945 to April 1957 (scanned issues are listed online here) researching… the history of the Shackelford family. Good hunting! 🙂

A Voynich presentation at Oxford Medieval Graduate Conference 2017…

by ⋅ 19 Comments

Well, here’s a thing. The Thirteenth Oxford Medieval Graduate Conference, to be held in a month’s time at Merton College (31st March 2017 to 1st April 2017) on the theme of “Time : Aspects and Approaches”, has a Voynich-themed paper in its Manuscripts and Archives session on the second day (11:30am to 1:00pm).

This is “Asphalt and Bitumen, Sodom and Gomorrah: Placing Yale’s Voynich Manuscript on the Herbal Timeline“, presented by Alexandra Marraccini of the University of Chicago. The description runs like this:

Yale Beinecke MS 408, colloquially known as the Voynich manuscript, is largely untouched by modern manuscript scholars. Written in an unreadable cipher or language, and of Italianate origin, but also dated to Rudolphine court circles, the manuscript is often treated as a scholarly pariah. This paper attempts to give the Voynich manuscript context for serious iconographic debate using a case study of Salernian and Pseudo- Apuleian herbals and their stemmae. Treating images of the flattened cities of Sodom and Gommorah from Vatican Chig. F VII 158, BL Sloane 4016, and several other exempla from the Bodleian and beyond, this essays situates the Voynich iconography, both in otherwise unidentified foldouts and in the manuscript’s explicitly plant-based portion, within the tradition of Northern Italian herbals of the 14th-15th centuries, which also had strong alchemical and astrological ties. In anchoring the Voynich images to the dateable and traceable herbal manuscript timeline, this paper attempts to re-situate the manuscript as approachable in a truly scholarly context, and to re-characterise it, no longer as an ahistorical artefact, but as an object rooted in a pictorial tradition tied to a particular place and time.

BL Sloane 4016 is a similar-looking herbal that Voynich researchers know well. Most famously, Alan Touwaide wrote a 500-page scholarly commentary on it (as mentioned in Rene’s summary of Touwaide’s chapter in the recent Yale facsimile). It dates to the 1440s in Lombardy, and even has a frog (‘rana’) on folio 81:

Marracini herself is an art historian who previously graduated from Yale, and who has an almost impossibly perfect set of research interests:

Her research focuses on Late Medieval and Early Modern scientific images, particularly alchemical and medical material, in England, Scotland, Germany, and the Netherlands. Her interests in the field also include book history and manuscript studies, Late Antique material culture, and the historiography of art, particularly in Warburgian contexts. Currently, she is writing on the history of Hermetic-scientific images and diagrams, and her work on Elias Ashmole’s copies of the Ripley Scrolls is forthcoming in the journal Abraxas.

All of which looks almost too good to be true. It’s just a shame her presentation falls on April Fool’s Day, so we’re bound to have people claiming that she doesn’t really exist and it’s all a conspiracy etc. 😉

Somerton Man – Two New Rubaiyat Scans…

by ⋅ 104 Comments

A few days ago, Australian robotics hacker Marcel Varallo (whose gladiatorial hacks making Roombas fight each other amuse me greatly) very kindly posted up two new scans of the Somerton Man’s Rubaiyat code (along with many megs of his collected Somerton Man stuff) on his blog.

I’ve put the three scans we now have on a Cipher Foundation Rubaiyat Code page, and strongly recommend that people use one of the new scans as a basis for doing any image processing work, rather than the one that has been on the Internet for years.

For example, if you put the three scans’ “Q” shapes side by side and try doing image processing experiments on them…

…what you find is that the so-called “microwriting” (found in the leftmost of the three images) was simply a quantizing artefact introduced when the original JPEG image had its brightness and contrast adjusted. With the new (slightly higher resolution, and generally much smoother) scan, all that nonsense disappears. There is no ‘microwriting’ there at all: The End.

Voynich entropy, transcription, and parsing…

by ⋅ 19 Comments

Voynich researchers without a significant maths grounding are often intimidated by the concept of entropy. But all it is is an aggregate measure of how [in]effectively you can predict the next token in a sequence, given a preceding context of a certain size. The more predictable tokens are (on average), the smaller the entropy: the more unpredictable they are, the larger the entropy.

For example, if the first order (i.e. no context at all) entropy measurement of a certain text was 3.0 bits, then it would have almost exactly the same average information content-ness per character as a random series of eight different digits (e.g. 1-8). This is because entropy is a log2 value, and log2(8) = 3. (Of course, what is usually the case is that some letters are more frequent than others: but entropy is the bottom line figure averaged out over the whole text you’re interested in.)

And the same goes for second order entropy, with the only difference being that because we always know there what the preceding letter or token was, we can make a more effective guess as to what the next letter or token will be. For example, if we know the previous English letter was ‘q’, then there is a very high chance that the next letter will be ‘u’, and a far lower chance that the next letter will be, say, ‘k’. (Unless it just happens to be a text about the current Mayor of London with all the spaces removed.)

And so it should proceed beyond that: the longer the preceding context, the more effectively you should be to predict the next letter, and so the lower the entropy value.

As always, there are practical difficulties to consider (e.g. what to do across page boundaries, how to handle free-standing labels, whether to filter out key-like sequences, etc) in order to normalize the sequence you’re working with, but that’s basically as far as you can go with the concept of entropy without having to define the maths behind it a little more formally.

Voynich Entropy

However, even a moment’s thought should be sufficient to throw up the flaw in using entropy as a mathematical torch to try to cast light on the Voynich Manuscript’s “Voynichese” text… that because we don’t yet know what makes up a single token, we don’t know whether or not the entropy values we get are telling us anything interesting.

EVA transcriptions are closer to stroke based than to glyph based: so it makes little (or indeed no) sense to calculate entropy values for EVA. And as for people who claim to be able to read EVA off the page as, say, mirrored Hebrew… I don’t think so. :-/

But what is the correct mapping or grouping for EVA, i.e. the set of rules you should apply to EVA to turn it into the set of tokens that will give us genuine results? Nobody knows. And, oddly, nobody seems to be even asking any more. Which doesn’t bode well.

All the same, entropy does sometimes yield us interesting glimpses inside the Voynichese engine. For example, looking at the Currier A pages only in the Takahashi transcription and using ch/sh/cth/ckh/cfh/cph as tokens (which is a pretty basic glyphifying starting point), you get [“h1” = first order entropy, “h2” = second order entropy]:

63667 input tokens, 56222 output tokens, h1 = 4.95, h2 = 4.03

This has a first order information content of 56222 x 4.95 = 278299 bits, and a second order information content of (56222-1) x 4.03 = 226571 bits.

If you then also replace all the occurrences of ain/aiin/aiiin/oin/oiin/oiiin with their own tokens, you get:

63667 input tokens, 51562 output tokens, h1 = 5.21, h2 = 4.01

This has a first order information content of 51562 x 5.21 = 268638 bits, and a second order information content of (51562-1) x 4.01 = 206760 bits. What is interesting here is that even though the h1 value increases a fair bit (as you’d expect from extending the post-parsed alphabet with additional tokens), the h2 value decreases very slightly, which I find a bit surprising.

And if, continuing in this vein, you also convert air/aiir/aiiir/sain/saiin/saiiin/dain/daiin/daiiin to glyphs, you get:

63667 input tokens, 50387 output tokens, h1 = 5.49, h2 = 4.04

This has a first order information content of 50387 x 5.49 = 276625 bits, and a second order information content of (50387-1) x 4.04 = 203559 bits. Again what I find interesting is that once again the h1 value increases a fair bit, but the h2 value barely moves.

And so it does seem to me that Voynich entropy may yet prove to be a useful tool in determining what is going on with all the different possible parsings. For example, I do wonder if there might be a practical way of exhaustively / hillclimbingly determining the particular parsing / grouping that maximises the post-parsed h1:h2 ratio for Voynichese. I don’t believe anyone has yet succeeded in doing this, so there may be plenty of room for good new work here – just a thought! 🙂

Voynich Parsing

To me, the confounding beauty of Voynichese is that all the while we cannot even parse it into tokens, the vast modern cryptological toolbox normally at our disposal does us no good.

Even so, it’s obvious (I think) that ch and sh are both tokens: this is largely because EVA was designed to be able to cope with strikethrough gallows characters (e.g. cth, ckh etc) without multiplying the number of glyphs excessively.

However, if you ask whether or not qo, ee, eee, ii, iii, dy, etc should be treated as tokens, you’ll get a wide range of responses. And as for ar, or, al, ol, am etc, you won’t get a typical linguistic researcher to throw away their precious vowel to gain a token, but it wouldn’t surprise me if they were wrong there.

The Language Gap

The Voynich Manuscript throws into sharp relief a shortcoming of our statistical toolbox: specifically, its excessive reliance on our having previously modelled the text stream accurately and reliably.

But if the first giant hurdle we face is parsing it, what kind of conceptual or technical tools should we be using to do this? And on an even more basic level, what kind of language should we as researchers use to try to collaborate on toppling this first statue? As problems go, this is a precursor both to cryptology and to linguistic analysis.

As far as cipher people and linguist people go: in general, both groups usually assume (wrongly) that all the heavy lifting has been done by the time they get a transcription in their hands. But I think there is ample reason to conclude that we’re not yet in the cinema, but are still stuck in the foyer, all the while there is a world of difference between a stroke transcription and a parsed transcription that few seem comfortable to acknowledge.

Inside the Zodiac Killer’s (cryptographic) head…

by ⋅ 56 Comments

Given that the Zodiac Killer’s first big cipher (the Z408) got cracked so quickly, it shouldn’t really be a surprise that he used a slightly different system for his second big cipher (the Z340). What is (arguably) surprising is that whatever change he made to it has not been figured out since then.

But what was he thinking? What did he want from a cipher? And how might his needs have changed between Z408 and Z340?

The Z408

Ciphers are normally made to be as strong as practically possible, given the technological, time, and resource constraints that apply to both sender and receiver: and with the two main driving needs being privacy and secrecy. Note that these aren’t always the same thing: the way I usually describe it is that while sex with your husband is private, sex with your tennis coach is secret. 😉

And so the first thing I find cryptographically interesting about the Zodiac Killer is that he was creating a cipher from a slightly angle from either of these: and he certainly wasn’t trying to communicate in any normal sense of the word.

Rather, I think that the point of Z408 was to be taunting, and to demonstrate to the police that he was in control, not them.

So imagine the Zodiac’s probable fury, then, when little more than a week after his three Z408 cryptograms appeared in local newspapers (the Vallejo Times-Chronicle, the San Francisco Examiner and the San Francisco Chronicle), Donald and Bettye Harden were all over the front pages explaining how they had cracked them.

Didn’t they know who was supposed to be in control here?

What was worse, the Hardens hadn’t used cryptological hardware or even high-powered cryptological smarts. They’d just used the Zodiac’s egoism (they guessed the first letter was “I”) and his psychopathic bragging (they guessed he would use the word KILL multiple times) as keys to his cryptographic front door: and then marched straight in.

I think it’s fairly safe to expect that the Zodiac was pretty pissed off by this.

Note that the Hardens carried on trying to crack the Z340 for many years afterwards: according to their daughter, her “mother wrote poetry and was as absorbed in her writing as she became with the Zodiac codes. She worked on the second code on and off for the rest of her life.”

The Z340

Comparing the overall style of the Z340 with that of the Z408, there seems to be plenty of reasons to think that the two are, at heart, not wildly different from each other. And yet (as is widely known) all the big-brained homophonic solvers written since haven’t made any impact on the Z340 at all.

All the same, I think the second interesting thing to note is that the changes to the Z340 system were surely not made to defend against computer-assisted codebreaking (because that hadn’t yet happened), but rather to make the updated system Harden-hardened, so to speak.

What does this mean? Well, we can probably infer that the first letter of the Z340 is almost certainly not I (not that that helps us a great deal) and the Zodiac Killer must have done something to conceal or remove the KILL weakness.

But, in my opinion, that latter change would surely not have been a theoretically-motivated cryptographic adaptation (he was without much doubt an amateur cryptographer), but rather something pragmatic and empirical, perhaps along the lines of:
* adding a repeat-the-last-letter token
* add an LL token
* add an ILL token
* add nulls inside tell-tale words
* etc

But there’s a problem with all of these. In fact, there are several problems. 🙁

The Problems

The first problem is that I don’t currently believe any of the above changes are disruptive enough to explain what we see in the Z340.

The basic stats of the four main Zxxx ciphers are:
Z408: 408 symbols, from a set of 54 unique symbols. (Note: E has 7 homophones, AST have 6 each, IO have 5 each, N has 4, FLR have 3 each, DHW have 2 each, everything else has 1).
Z340: 340 symbols, from a set of 63. [Hence symbols/textsize is 18.5%, a fair bit higher than the Z408’s 13.3%]
Z32: 32 symbols, from a set of 30.
Z13: 13 symbols, from a set of 8.

It would be very tempting to suspect (as many people have) that the Z340 is ‘therefore’ just the same as Z408 but with 39% more homophones. Yet a problem with this popular hypothesis is that it should be well within range of automated homophone solvers, and to date they haven’t managed to make any impact.

A second problem is that the kind of homophone cycles that so characterized the Z408 seem to be largely absent in the Z340: and yet because the Zodiac Killer would not have had any clue that these were a technical weakness of his system, it seems unlikely to me that he would have adjusted his system to work around a weakness that he didn’t actually know was a weakness.

A third problem is that the Z340 has a fair number of asymmetries that don’t fit the it’s-a-straight-homophonic-cipher model. For example, lines 1-3 and 11-13 have (as Dan Olson pointed out some years ago) almost no character repeats.

There are yet other asymmetries: for example, while 63 different symbols appear in the top ten lines, only 60 appear in the bottom ten lines. And there’s the mysterious ‘-‘ shape at the start and end of line 10: and the odd-looking “ZODAIK” sequence on line 20.

One final asymmetry: the ‘+’ shape seems to function differently in the top and bottom halves – it is often preceded by ‘M’ in the top half, but never preceded by ‘M’ in the bottom half.

How does assuming the Z340 is a pure homophonic cipher explain any of these behaviours, let alone all of them?

Lines 1-3 and 11-13, revisited

I keep coming back to the 1-3 and 11-13 property as mentioned here. I think it’s important to say that Dan Olson’s conclusion (that “lines 1-3 and 11-13 contain valid ciphertext whereas lines 4-6 and 14-16 may be fake”) seems likely to be landing a little bit wide of the mark.

To me, this same property of these lines implies (a) that the homophonic versions for each letter were probably used in pure sequence here, but also (b) the homophone cycles were somehow ‘reset’ after ten lines (i.e. the homophone cycles all started again at the start of line eleven). And perhaps also that any characters repeated in the first three lines are rarer characters, rather than the homophone-friendly ETAOINSHRDLU etc.

It might even be that the Zodiac Killer kept on adding homophones as he constructed the cipher UNTIL he had three lines’ worth of essentially unique homophones: that is to say, that the three line blocks in 1-3 and 11-13 are how his system made the choice of the number of homophones, rather than as a consequence of the number of homophones he chose. Nobody has yet (to my knowledge) satisfactorily explained where he came up with his homophonic allocation for Z408: certainly, searching for this in crypto books hasn’t yielded any likely candidates.

Could it be that the Zodiac Killer worked backwards from his actual Z408 ciphertext to determine the number of homophones, rather than worked forward from the number of homophones to the ciphertext?

—

Update: I received the following off-line comment from David Oranchak, but thought it better to update it within the post itself…

Nick, there are a few other seemingly rare phenomena that can be observed in Z340. I’m curious what you think of them.

The first is the pivots:

http://zodiackillerciphers.com/wiki/index.php?title=Encyclopedia_of_observations#The_.22Pivots.22

Those kinds of patterns are difficult to arise by chance, so they are suspected to be some sort of feature of the encoding scheme.

Z408 is littered with repeating bigrams but Z340 seems to have fewer than would be expected via normal homophonic encipherment of a plaintext in a normal reading direction. However, the bigrams show up again if you consider a periodic operation on the cipher text:

http://zodiackillerciphers.com/wiki/index.php?title=Encyclopedia_of_observations#Periodic_ngram_bias

The count of 25 repeating bigrams jumps to 37 or 41 or even higher, depending on the periodic operation applied to the cipher text. Here is a tool that illustrates the various operations:

http://zodiackillerciphers.com/period-19-bigrams/

You’ve already identified the seemingly rare phenomenon of rows that lack repeating symbols. There are 9 such rows. In 1,000,000 random shuffles of Z340, none had that many rows. In fact, the best that was found was 8 rows which occurred in only 12 of the shuffles.

Your “M+” asymmetry observation seems to fit in with the general observation that repeating bigrams are phobic of certain regions of the text. The lower left, for instance, seems to hate bigrams: http://zodiackillerciphers.com/images/z340-repeating-bigrams.png

Another really strange observation is the distribution of non-repeating string lengths. For each position of Z340, measure how far you can read forward without encountering a repeating symbol. You end up with a string with unique sequences of length L. Jarlve found that for Z340, there is a peak of 26 occurrences of unique sequences of length 17 (which happens to be the width of Z340). It is really interesting that in random shuffles, this phenomenon is only observed on the order of one in a billion shuffles.

Finally, I would recommend that anyone interested in this topic should check out this thread on morf’s Zodiac forum: http://zodiackillersite.com/viewtopic.php?f=81&t=3196 Especially the more recent posts on the latter pages. “Jarlve” and “smokie” in particular are doing fantastic work exploring various transcription schemes that could explain the various curious features of Z340 (in particular, the relationships between periodic bigrams and transposition schemes).