I’ve been thinking a little more about how to go about cracking Scorpion Cipher S5.
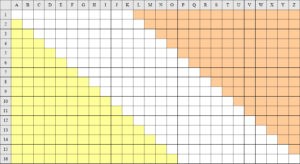
I mentioned before that I thought that the encipherer might well have started from an elegant-looking 26×16 grid filled with diagonally-downward families of shapes, and that this arrangement might offer codebreakers some additional kind of “spatial logic” to support their efforts that traditional ciphers don’t usually provide.
From the letters that accompanied the ciphertexts, my inference is that the Scorpion is like a smart 12-year-old who has just ‘got’ the elegance of maths: but this leads me to a secondary inference that he/she probably didn’t understand modulo addition, because if he/she did, then we would surely have seen more 16-element shape families in the text.
I’ll explain with the help of a diagram of the kind of 26×16 grid I’m talking about:
If the encipherer had laid out his/her grid with modulo-26 maths in mind, then 16-element families that start in the orange (top right) area and step diagonally down and to the right (as I predict) should wrap around (modulo 26) to the yellow (bottom left) area. However, I believe that we don’t see nearly enough length-16 shape families to support that grid-filling model.
What I think actually happened was that the encipherer only started length-16 families in the A-K range for alphabet #1, which would have ended on P-Z for alphabet #16. This means, for example, that because the ‘dice’ family (actually, the ‘dots in a square’ family, to be precise) has members in alphabets 1, 3, 4, 8, 9, 12, 14, and 15, we may well be able to directly infer that its very first member (in alphabet #1) is A-L.
Moreover, given that the lowest frequency letters in the encipherer’s accompanying letters are…
k : 0.4%
x : 0.3%
j : 0.1%
z : 0.0%
q : 0.0%
…we may also be able to make a reasonable guess as to which possibilities of A-L are the least likely. For example, because the dice family appears in columns 1/3/4/8/9/12/14/15 (of the 16-column sequence I discussed before), this would map to:
+0 : ACDHILNO --- OK
+1 : BDEIJMOP --- has J, so fairly unlikely
+2 : CEFJKNPQ --- has J, K and Q, so not likely at all
+3 : DFGKLOQR --- has K and Q, so not likely
+4 : EGHLMPRS --- OK
+5 : FHIMNQST --- has Q, so not likely
+6 : GIJNORTU --- has J, so fairly unlikely
+7 : HJKOPSUV --- has J and K, so not likely
+8 : IKLPQTVW --- has K and Q, so not likely
+9 : JLMQRUWX --- has J, Q and X, so not likely at all
+10: KMNRSVXY --- has K and X, so not likely
+11: LNOSTWYZ --- has Z, so not likely
So in fact, I suspect that we already know enough to guess that the dice family members encipher either ACDHILNO or EGHLMPRS (in sequence), which I think isn’t a bad starting point at all.
Finally, I suspect there’s something of a cryptological paradox in play here: the more alphabets are involved, the more spatial structure we have to work with. Hence S5’s 16 alphabets might well make it surprisingly crackable. 🙂
That’s actually very nice, it could explain why there are symbols which fit in to families which seem like they would have fewer than 16 members.
I still think it doesn’t quite answer why some symbols from the same family appear in the same column. That would put them horizontally on your chart, not diagonal.
Can we apply ideas of how to reverse engineer S5 to S1? If I remember, it appears to have a 5-cycle period but it seems inexact which makes me think there are either nulls or encoding errors. Either way, the text with S5 claims that S1 is simpler, and it appears to share some properties.
ponky: it sounds paradoxical, but I suspect that S5’s greater regularity makes it more crackable than S1, as long as some basic organizing principle was used. I’m not too worried about the details, because spatial reasoning – such as I outlined for the family of dice-like shapes – might well constrain the solution much more strongly than traditional logic, if only we can get our heads round it. 🙂