Voynich cipher structure…

What (in my opinion) has scuppered just about every code-breaking assault on the VMs to date has been the faulty presumption that you don’t need to worry about anything so boring as “getting the history right first”, because the statistical analysis fairy will fly in waving her +10 Wand of ANOVA and somehow sort it all out. Errrm… won’t she?

Yet even as early as 1931 John Matthews Manly pointed out that the Voynich Manuscript’s quire numbers were clearly written in a 15th century hand – hence it couldn’t easily post-date 1500. So why do people still persist in using their stats tricks to hunt for complex mechanisms (such as Vigenère polyalphabetic ciphers, and even the dreaded Cardan grille – though personally, I’d rather have a nice mixed grille) that weren’t invented till nearly a century later? Whatever cryptographic arrangement you propose yielded the VMs’ distinctively structured behaviour should be consistent with the limited palette of techniques available to a cipher-maker circa 1450-1500.

In short, history says (whether you choose to listen to it or not) that we shouldn’t hypothesize some single high-powered cipher trick – rather, we need to look for a set of simple techniques consistent with Quattrocento knowledge of cryptography blended together in a devious (and probably subtly deceptive) way.

Even so, 50 years of statistical hackery later, it seems pretty clear that the cryptographic stats fairy hasn’t worked her spell as hoped. But why should her (usually pretty good) magic have failed so abysmally?

Well… if you delve a little deeper into theoretical statistica, you find the theorists’ nimble “get-out clause” – that the presence of so-called confounding factors can disrupt all the neat assumptions underlying stats’ mathematical models. These factors, in a nutshell, are ways in which individual samples within your overall dataset are causally linked together locally in non-obvious ways that make the global numerical tests go wrong… really quite badly wrong, in fact.

Unsurprisingly, I believe that the presence of confounding factors is precisely the reason that the standard statistical toolbox continues to draw so much of a blank with the VMs – that is, the individual letters / glyphs are silently linked together in ways that act as local confounding factors to any global analytical pass. But if so, what exactly are those pesky linkages?

My conclusion is that the bulk of the, errrm, ‘confundity‘ arises because the “vowel” glyphs (a / e / i / o / y) are like many Budapest workers – they only get to pay their rent by holding down two or more different jobs at the same time (though normally only one job at any given moment). For example, I don’t believe that the “o” in “qo” has anything at all to do with the “o”s in “ot”, “or” or “ol” (you can tell this because “qol” only pops up in those later sections where you find free-standing “l” glyphs). Similarly, I don’t think the “a” in “aiin” is in any way linked with the “a” in “al”, or even with the “a” in “aiir” (because their usage and context patterns are so different).

Yet once you fully accept that this is the case, you’re more or less forced to follow a long path of uncomfortable reasoning that leads you right to the doorstep of an even more uncomfortable conclusion: that the cover cipher is largely formed of groups of letters. Which is to say, that a / e / i / o / y have no independent meaning except as part of the letters with which they are immediately paired or grouped, and that the Voynichese CVCV structure (to which linguists have clung for so long through a storm of criticism) is not definitive evidence of the presence of language, but is instead an artefact of the cipher system’s covertext – merely its misleading outer appearance, not its inner structure at all.

Furthermore, the VMs’ cunning encipherer occasionally adds in a “space-transposition cipher” after his “pairification” stage to prevent repetition of the pairs becoming just that little bit too obvious for his liking: for example, on page f15v, the first line’s “ororor” has been turned into “oror or“, while the second line’s “orororor” has been turned into “or or oro r“. To my eyes, the underlying sequential repetitions look very much as if the plaintext contains the oh-so-familiar “MMM”, “CCC”, “XXX” or “III” of Roman numbers, even circa 1450 a pattern so visually obvious to codebreakers that the verbose cipher system needed to be hacked yet further to conceal it.

Hmmm… four repeated Roman number letters, and four pairs in the or / ol / ar / al set apparently to hide repetitions – a coincidence? Or might it be that or / ol / ar / al in some way encipher m / c / x / i (though probably not in that order)? Well… I would be hugely unsurprised if this miniature four-pair cipher system turns out to have been designed specifically for this purpose in an earlier cipher, and that the mechanism was reused and adapted for the later (and far more complex) Voynichese cipher system that evolved out of it – that is, it remained in the encipherer’s personal cipher alphabet rather like a “cryptographic fossil”. (As a general aside, the idea that Voynichese popped into existence fully formed in the shape we now see it makes no engineering sense at all to me – something as tricksy and structurally complex must necessarily have gone through a fair number of stages of evolution en route.)

Incidentally: with spaces included, you see olol (51), arar (47), alal (37) and oror (23) – but take spaces out, and you get olol (186), arar (161), oror (87), alal (60), ololol (13), ararar (7), ororor (1), alalal (1)  and the orororor (1) mentioned above. At the same time, remove all the spaces and you see just four instances of okok and two of otot in the entire VMs, i.e. ol is followed by ol more than 50x more often than ok is followed by ok.

To be sure, this does not explain all the behavioural properties of Voynichese: ultimately, repetitive phrases like “qokedy qokedy dal qokedy qokedy” (and “ur so qokedy daiin, m8 lol“?) are dancing to a quite different underlying beat. Whatever kind of token gallows characters turn out to encipher, I think it is extremely unlikely that they are a single letter substitution – some other kind of enciphering mechanism is going on there (I suspect some kind of in-page transposition cipher). Similarly, I’m pretty sure that “qo”, “d”, and “y” encipher tokens of a quite different nature again (here, I suspect that they match the three basic abbreviatory shorthand marks that were in active use in the Quattrocento, i.e. “qo” => subscriptio, “d” => superscriptio [macron], and “y” => truncatio).

Arrange all these smaller systems together, and I think that what is revealed is a multi-stage cipher architecture looking broadly like this:-

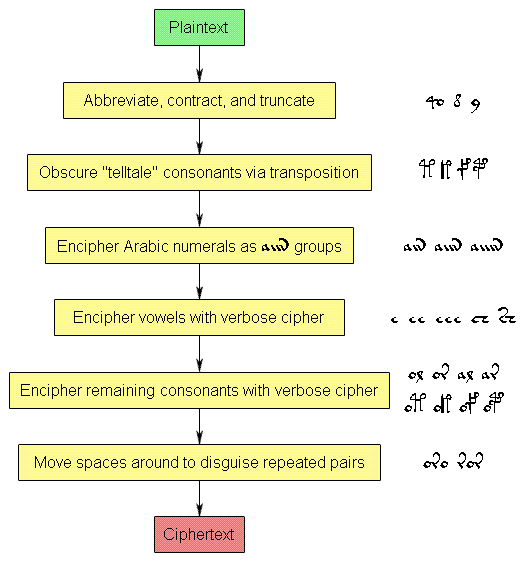
Now, I’ve had flak from a number of people over the years (ummm… mainly Elmar, truth be told, bless ‘im) who comment that this kind of arrangment seems far too complex to be right. The problem I have is how to convince such naysayers that what I present here is the end result of a basically sensible methodology – that of decomposing the heavily-structured nature of Voynichese into its constituent pieces, each of which is consistent with the (relatively low) level of cryptographic technique available before 1500. That is, the real cleverness we are up against here isn’t one of fiendish mathematical complexity, but of cunning arrangement of simple pieces – not of Albertian innovative technique, but of Filaretian innovative architecture.

All the same, even the best-designed house needs walls and a roof – and here, the main cipher properties arise from the use of verbose cipher to make a language-like covertext. Get around that, and I the rest of the structure’s secrets may very well yield to the repetitive numerical prodding that is statistical analysis. Here’s how to do it:-

(1) write a simple text filter to undo the space transposition cipher:-
–> (a) get rid of any spaces between [o | a] and [l | r] – i.e. transform “oro ror” into “ororor”
–> (b) get rid of any spaces between [or | ol | ar | al]  and [or | ol | ar | al] – i.e. transform “or al or” into “oralor”

(2) tokenize the text into the following units, making sure that you tokenize “qo” before anything else (i.e. “qok” must tokenize to “qo” + “k”, and not to “q” + “ok”). Of course, I may have got the precise details very slightly wrong, but I’m pretty sure that this is not less than 90% of the way there.

qo
eeee, eee, ee, ch, sh
ok, ot, of, op, yk, yt, yf, yp
ockh, octh, ocfh, ocph, yckh, ycth, ycfh, ycph
ol, or, al, ar, an, am
air, aiir, aiiir, aiiiir
ain, aiin, aiiin, aiiiin
aim, aiim, aiiim, aiiiim
ckh, cth, cfh, cph
eo, od  <--- these two are the wobbly ones that may need further thought!

Note that a number of additional single-letter tokens get left over (most notably s, d, y, l, k, t, f, p), but these are not paired, so that’s OK. My guess is that any left-over “o” and “a” characters are probably nulls or pen-slips.

(3) perform your statistical analyses on the set of (roughly 50) tokens output by stage 2.

Note that I don’t believe that this somehow “solves” Voynichese in a single step (becaus nothing connected with the VMs has ever been that simple before, and that is unlikely to change now). However, I do believe that removing the pairs like this removes arguably the most problematic set of confounding factors from the text, and hence that doing so should allow the productive use of statistics to crack the rest of the cryptographic problems associated with Voynichese.