Long-suffering Cipher Mysteries readers will no doubt recall various recent posts here about the Hollow River Cipher. Though I had a lot of fun decrypting the word “TREASURE” (that’s something that’s not going to happen to many cipher people, let’s face it), it then turned out that I wasn’t actually the first person to decrypt it. Furthermore, it may well be that some (or indeed all) of the stories around the cryptogram are concocted faux histories.

However, much as with the Beale Ciphers, even if I happen to heartily distrust all the nonsense layered on top of it, I don’t (yet) see any reason to doubt the cipher itself.

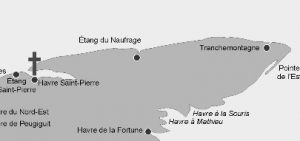
Anyway, there’s a particularly interesting word in the plaintext that needs a bit of context in order that it can be understood properly: NAUFRAGE.

Île Saint-Jean – 17th Century

For the Mi’kmaq people, the island was Epekwitk, “Cradle on the waves”. The first Europeans to the island were the French (Cartier briefly visited it in 1534): though Champlain mentioned it in 1603, it didn’t appear on his 1604 map. Even in Champlain’s 1612 map it was little more than a speck, but by the time of his 1632 map it was the proper size, shape and named “l’Ile Saint-Jean”. In HHGTTG terms, “Mostly Harmless”, one might say. 😉

Through the 17th Century, the island was owned (among a number of others) by Nicolas Denys, “La Grande Barbe”, who was a famous entrepreneur and merchant-industrialist. However, his interest was more in fishing rather than establishing any kind of colony. All the same, Denys was more than a little put out when in 1663, Sieur François Doublet was given the island, in return for paying an annual rent to la Compagnie de la Nouvelle-France. However, when Doublet died not long after, his plans to colonise the island fell to pieces. A similar attempt (by Gabriel Gautier) to establish a fishing presence on the island in 1686 also came to naught, despite several expensive attempts.

Île Saint-Jean – 1700-1763

The Treaty of Utrecht in 1713 left the island as a French possession, but attempts to colonize it failed, according to Thomas Caulfield in a letter of 16th May 1716. However, the first reasonably successful colonization began around 1719, when a group of settlers were shipwrecked on the North-East coast, at a place subsequently called “Naufrage” (‘shipwreck’). A 1721 letter by De la Ronde mentioned twenty families settled at port Lajoie, and ten more at Tranchemontagne (South Lake), Saint-Pierre (St Peter’s) and Tracadie.

From that starting point, the population of Île Saint-Jean grew as the century proceeded. However, both the British and French forces were fighting for control over the wider area. Following the Siege of Louisburg (1745) [Louisburg was the main town of Île Royal, Cape Breton Island] by New Englander forces, the population of Île Royal was forcibly deported to Europe, though the settlers on Île Saint-Jean (now called Saint John’s Island) was left in place.

But with the Treaty of Aix-la-Chapelle in 1748, both Île Royal and Île Saint-Jean were returned to the French, in return for Madras and France’s withdrawal from the Low Countries. Claude-Élisabeth Denys de Bonaventure returned to Île Saint-Jean in 1749 with a thousand new settlers, all hoping for a fresh start.

However, 1749 was when Father Le Loutre’s War began: this was a long process whereby the British governors of Canadian provinces would make life progressively closer to intolerable for French settlers. This led to a steady flow of disenchanted settlers moving from the mainland to the safer haven of Île Saint-Jean. This process then peaked in 1755, with mass expulsions of Acadian settlers, many of whom ended up on Île Saint-Jean as well.

The end-game arrived in 1758, when Lieutenant-Colonel Andrew Rollo (the 5th Lord Rollo, aristocracy trivia fans) was sent with 500 troops to secure the island, and to then deport everyone on it to Europe. About 1200 of these deportees died aboard those transport ships: it was a miserable end to what had become a horrible era.

In 1763, the island – now firmly under British control – had its name changed to Prince Edward Island, which is what it has stayed ever since. (Though personally, I have a bit of a soft spot for Epekwitk.)

Naufrage, Revisited

If we go back to the Hollow River Cipher, the date at the top places it firmly at the time of the main French colonization, when the island was Île Saint-Jean:

F R E N C H   S L O O P   L ['] A I [G] L E    [= Most likely plaintext]
G U L F   S T   L A W R E N [C] E   M A Y 10, 1738

The cipher author also tells us the specific place he’s interested in:

L E A G U E  W E S T  N A U F R A G E

From what we now know, ‘naufrage’ isn’t (as I first thought) a shipwreck, but is actually the place Naufrage (i.e. named after the 1719 shipwreck).

Naufrage is mentioned in a 1752 census, which was turned into a map for a 2008 exhibition at the Acadian Museum (online here):

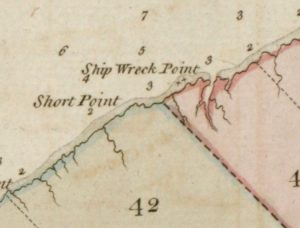
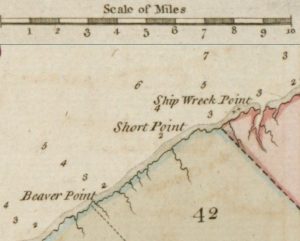
The same name persisted (Anglicized as “Ship Wreck Point”) in a 1775 map:

Perhaps most interestingly, Étang du Naufrage is mentioned in a 1760 book by Thomas Pichon with a horrendously long title, which describes a picturesque 1752 journey around Île Saint-Jean that the author had taken:

Nous continuâmes notre route en côtoyant la mer pendant six lieues jusqu’à l’étang du naufrage. Cette côte, quoi qu’assés unie, ne presente à la vûe que desert où le feu a passé, et plus avant les terres sont couvertes de bois franc. Un seul habitant que nous trouvâmes, nous assura que les terres des environs de l’êtang sont très bonnes, aisées à cultiver, et que tout y vient en abondance. Il nous en donna une preuve qui nous fit plaisir, c’étoit le peu de froment qu’il avoit eu la faculté de semer cette année là; effectivement rien n’étoit fi beau que ses épics qui étoient plus gros, plus longs et mieux garnis que ceux d’Europe.

Ce fut à l’occasion d’un naufrage qu’un batiment François fit sur cette côte, qu’on a donné à l’étang le nom d’Etang du naufrage. Quelques passagers, après que le vaisseau se fut perdu à quatre lieues en mer, se sauverent sur des débris et furent les premiers qui s’établirent au havre Saint Pierre. Au reste l’étang s’enfonce un quart de lieue dans les terres au sud-ouest. Sa largeur à son extremité est d’une portée de canon de quatre livres de balle. Il s’y décharge un grand ruisseau qui ne tarit jamais, parce qu’il est entretenu par deux sources qu’on trouve à deux lieues et demie dans les terres d’ouest sud-ouest. Ce ruisseau peut fournir assés d’eau, presqu’en tous tems et malgré les gelées à plusieurs moulins qu’on y a construit.

La côte depuis le havre de la fortune jusqu’à celui de Saint Pierre où nous arrivâmes le 14 Aoust après avoir encore côtoyé pendant six lieues depuis l’étang, […]

Translated roughly (by me, so expect fluency rather than accuracy):

We continued on our journey, coasting six more leagues around the island to the étang du naufrage. This place […] looked like the empty space you get after fire has cleared it, and beyond that the lands are covered with hardwood. One inhabitant whom we found assured us that the lands around the étang are very good, easy to cultivate, and that everything is in abundance. As proof, he showed us a little wheat he had been able to sow that year; indeed, nothing was as beautiful as its ears, which were larger, longer, and better than those of Europe.

It was on the occasion of a French shipwreck on this coast that the étang was given the name of étang du naufrage. Some passengers who had clung to the debris after their ship had been lost four leagues out to sea, ended up becoming the first settlers at St. Peter’s Harbour. The étang itself extends a quarter of a league into the lands to the southwest. At its widest, its width is the range of a four pound cannonball. A large brook discharges into there: this never runs dry because it is maintained by two springs, which are found two and a half leagues west-southwest. This brook provides a water supply to several mills that were built there, almost at all times and despite the frosts.

The coast from le havre de la fortune to that of St. Peter where we arrived on 14 August after having travelled for six leagues from the étang, […]

“League West Naufrage”…

So: now that we know exactly where Naufrage is, we also know that the cipher author is directing us to go one league west from there. But… how far is a league?

This is, of course, one of those niggly questions that gets historians sighing heavily, because different people at different times and different places had different answers.

For an Englishman of the 18th Century, a league on land was three miles, while a league at sea was three nautical miles (~3.4 miles). But I have to also point out that our cipher author was on a French ship, and a French league (lieue de Paris) was standardized in 1674 as 2000 toises (~2.4 miles), and then in 1737 (the year before the cipher’s date) as 2200 toises (~2.66 miles).

Yet even the yardstick (leaguestick?) we have in Pichon’s account – that it is six (presumably French?) leagues from Naufrage to Saint Peter’s Bay, which is about 24 miles / 36 kilometers by sea (because you have to double back on yourself) – isn’t much help, because it would give a figure of 4 miles per league. So unless the geography around Saint Peter’s Bay has changed much in the last couple of centuries, Pichon’s ability to estimate distances in leagues seems to have not been as good as he imagined.

Adding all these classes of inaccuracy together, it seems likely to me that the least and most ‘one league’ could be in practice are about 2 miles and 4.5 miles respectively. So: how does this stack up with the (now widely presumed) identification of the same location with the Hollow River?

The location given for Hollow River by the local government is 46°28’00.0″N 62°30’00.0″W . According to Google Maps, this runs alongside the modern Swallow Point Road, and its mouth is about 6.8km (4.2 miles) from the mouth of the Naufrage étang. So Hollow River would seem at first to be a reasonable guess.

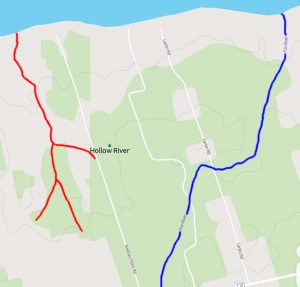
If we look at MapCarta’s Hollow River page, we can see two modern candidate rivers – Hollow River and Fox River, which I’ve highlighted here in red and blue respectively:

Now, remembering that the cipher says…

ONE HUNDRED AND ELEVEN YDS UP SMALL STREAM

…which is this small stream to be, Hollow River (6.8 km along from Naufrage) or Fox River (5.6km along)? I have to say that Fox River, if it was around in 1738, would seem to be a better candidate than Hollow River. And there’s even Cow River, which is a mere 2.2km along from Naufrage. So let’s look more closely at the 1775 map:

Here, we can see a decent-sized stream heading South from just below the ‘n’ of “Short Point”, marked as being ~3.5 miles (5.6km) from the mouth of the Naufrage étang, which I think lines up exactly with the modern Fox River. The next reasonable size stream along would seem to be the slightly smaller-looking stream to the right of “Beaver Point”, but this would seem to be about 5.5 miles (8.8km).

So it would seem from this historical detective work (a) that Hollow River didn’t even properly exist in 1775, (b) that calling it the Hollow River Cipher may well have been based on a misidentification from a century ago, and (c) that the stream we should be actually interested in is the modern Fox River, which appears to be the first reasonable size stream about a league west of Naufrage on the 1775 map.

“ONE HUNDRED AND ELEVEN YARDS”?

At this point I should add that 111 yards is pretty close to 50 toises (French fathoms, i.e. 2.131 yards x 50 = 106.5 yards), so I’m guessing that the cipher author heard the French sailors talking about going “cinquante toises” down the “petit ruisseau”.

Where would 111 yards down the Fox River take us? If we have a look in Google Maps, the satellite image shows us where (I’m pretty sure) the Fox River is (the first white dot down marks 100m or so from the end, which is pretty close to 50 toises):

The rest you can figure out, I’m sure. 🙂

Finally: why take treasure up a small river, you may ask? The answer would seem to be painfully obvious: that those wanting to conceal it would want to carry it as far inland on a small boat as they easily could.

In that respect, these people would seem to be brothers-in-(yard)arms to Bernardin Nageon de l’Estang (operating at the same time, though in a different ocean entirely), who wrote that he had hauled his treasure up a small creek, also presumably in a small boat. Wouldn’t it be nice if something were still there, in both cases? Not hugely likely, for sure, but a nice thing to dream about all the same.

PS: for more on the history of Île Saint-Jean in French, I found the following two articles (this one and this other one) very helpful indeed.

Update: 1752 Census entry

While looking (unsuccessfully) for decent French maps of the island, I found a nice webpage containing a detailed 1752 census of Île Saint-Jean, The census taker (Sieur de la Roque) travelled round the island on land. (The French original can be found here.) It may well be that he travelled with Thomas Pichon, because they both seem to have had the same conversation with the (unnamed) settler at Naufrage.

At Pointe de l’Est:

Next, after making another two leagues, we doubled Pointe de l’Est. This point had been reduced to a wilderness by a fire which has passed through this section, and the settlers have established themselves at a distance of two leagues from the point on the north side. The land upon which the people have settled is of the best for cultivation. Nevertheless they have sown no seed here, and the truth is that they lack the seed to sow, and if the King does not make them a gift or a loan of seed so that they can sow it next spring they will find it impossible to maintain themselves, being today at the last stage of poverty through the great mortality among their live stock.

He then moved on to Naufrage:

We left on the 13th and took the route for l’Etang du Noffrage, following the sea shore continually for the six leagues at which the distance from the Post at Pointe de l’Est to l’Etang du Noffrage is estimated. In this distance we met with nothing worthy of notice. The land is a desert owing to the occurance of the fire, but a short distance inland the country is covered with hardwood and the soil was good for the production of all kinds of grain and roots; everything coming up in abundance. Owing to the lack of seed grain the settler here was unable to seed his land this year, but the small quantity of wheat which he was able to sow is amongst the finest in the Island. The ears are long, large, and well filled. The Etang du Noffrage runs a quarter of a league inland to the south-west. The breadth averages 80 toises. At the extremity of the étang, a long brook, which never dries up, discharges its water. This brook is supplied from two large springs lying at a distance of two leagues and a half inland to the west-south-west. The brook contains sufficient water to run flour and saw mills, but as regards the latter they are considered useless as there is no timber suitable for sawing, all the hardwood, growing in the surrounding district being good, at best for the building of boats. We left on the 14th for St. Pierre du Nord. We counted the distance between the two points as six leagues by the road. We saw nothing on the way that calls for a description.

Update #2: Île Saint-Jean Forestry

Anyone who wants a list of sources of pre-1760 writing on Île Saint-Jean would be well advised to look at “Early Descriptions of the Forests of Prince Edward Island: A Source Book” by Douglas Sobey. “Part I: The French Period – 1534-1758” is online here.

I’ve had an intriguing email from Cipher Mysteries commenter Paul Relkin concerning the Hollow River Cipher.

He had thought to contact Linda Outcalt, whose (inverted) photograph of Sterling Ramsay was on the cover of his book “folklore prince edward island”. (Though the book credits only mention Hilda Woolnough.) Ms Outcalt suggested he should instead contact Harry Holman, “a prominent archivist for the Prince Edward Island government”. Paul continues:

This was a great suggestion! Mr. Holman was not only familiar with the Hollow River Cipher but he was able to produce documentation from a local newspaper establishing that the cipher was actually solved many years ago. He also provided some excellent commentary about the story behind the cipher. He has given me permission to share this with Cipher Mysteries on his behalf.

Here’s what Harry Holman wrote:

Harry Holman on Hollow River…

I have read your postings on Cipher Mysteries with interest but am afraid I must challenge your claim of being the first to decipher the coded message appearing in the Prince Edward Island Magazine. I have found evidence from 1935, and republished in 1946, that the message was deciphered by Blythe Hurst, a school teacher, naturalist and author who wrote under the pen name “Agricola.” The solution was published in the Charlottetown Guardian newspaper on 20 April 1935 p. 12 and again on 20 April 1946 p. 9.

My initial thought was that Hurst might have been connected with the appearance of the original Prince Edward Island Magazine article but it appears he immigrated to Prince Edward Island only in 1910. While he does not publish the entire text of the message it is clear that he has identified the key for interpreting the message and the main elements have been revealed.

As to the original PEI Magazine articles, it is important to place the publication in context. The Magazine, which ran from 1899 until 1905 provided a forum for a great many authors, many of who were identified only by initials or by pseudonyms. While it contained a number of high-quality and well-researched historical articles it was also a platform for a flourishing creative writing community. Many of the fiction pieces picked up on themes popular at the time. Ghost stories based on historical incidents seemed to strike a particularly responsive chord with readers. Only last week I wrote of the background of one of these, The Ghost of Holland Cove.

In that case the author was identified, but I have little doubt that the submissions by “Senachie” and “D.A.W.” are of the same character. A hint may be that the Gaelic basis of Senachie is “professional storyteller”

While a scattering of facts is essential to establish the credibility of historical fiction, a super-abundance of them is evidence of a fabrication. Such is the case here – especially in the supposed “back story” supplied by DAW. While Hollow River is a real place it is an unlikely setting for such an elaborate tale. I have been there and it is hard to imagine an area less likely to be chosen as a cache for guns and treasure. In the late 1730s it was entirely uninhabited although there was some French settlement at Naufrage to the east of the site. The river itself is a mere trickle emptying across a thin strip of sand which is backed by rocks and cliffs. It was one of the last areas of the colony to be settled and a road did not run through the thinly settled area until the 1830s. By the beginning of the 20th century the shore road had been abandoned and a new line of road dating from the 1860s or 1870s was in use.

The use of the multiply layered narrative was a common literary device during the period at the end of the 19th century. Here we have an account of an alleged diary entry recounting a mysterious note in a bottle telling of an incident. All the accounts lack credibility and have errors of fact or interpretation. The language used in the diary entry is quite unreflective of the actual writing of the mid 18th century. I have read a number of diaries from the period and they read nothing like this and the form and content is quite an anachronistic and imaginative interpretation of how a diary of the period might read.

I note that a number of contributors to the Cipher Mysteries website have raised practical objections to the facts of the story including the difficulty and pointlessness of transferring cannon to a barren shore. I think that such objections could be raised to almost every assertion made in the account but I do not think it necessary to parse it further.

For these and many other reasons I conclude that the Hollow River mystery is almost certainly a complete fabrication. The cypher message appears to be merely a “brain teaser” created by the author of the story and is unlikely to have any factual basis.

Without a single documentary support the pyramid of “facts” crumbles, but that has not prevented the story from being included in anthologies of ghost stories and folklore, particularly of the uncritical sort.

Thank you for reminding me of this tale.

Nick’s Further Thoughts…

The reason that I find cipher mysteries – long-unsolved historical ciphers where even the history surrounding them is suspect – so head-shakingly fascinating is that it can be ridiculously hard to tell the true, the false, and the merely hopeful apart. The (almost entirely false) Beale Papers wrapped around the (probably entirely genuine) Beale Ciphers form a case in point.

For the Hollow River Cipher, I share with Harry Holman many of the same doubts about the (supposed) diary entry: moreover, I think it no less likely that many other (supposedly meshing) parts of the story as presented in the PEI Magazine could have been camp-fire confabulations, back-filled around the same core cipher.

In fact, if someone were to propose to me that – more or less exactly mirroring the Beale Ciphers and Beale Papers – the Hollow River Cipher itself was genuine but that everything else wrapped around it was fake (perhaps in the spirit of multiple contributions to the same lightly-literary pirate-ghost jest), I’d be hard-pressed to demur.

And so I now find myself in the same awkward position with both the Beale Cipher and the Hollow River Cipher: that while I’m not enough of a Cipher True Believer for armchair treasure hunters (who seem to want every scrap of evidence to be true), I also seem to have more faith in the ciphers themselves than people who are comfortable writing all the evidence off in one go as no more than a long-running in-joke.

Though Holman handily highlights the presence of a super-abundance of facts (I certainly didn’t know that the settlement just East of the site was called Naufrage), this would surely seem to be more of a witness for the defence than for his prosection. In many ways, perhaps it should be best taken as an epistemological red flag to us all, signalling that we instead need to look and think more clearly at the different accounts making up the picture, to see which (if any) are true, false, or merely amusing or hopeful.